Konstruktionsprinzip
Curved Kites
Die Kollektion Curved Kites zeigt Anordnungen einer Serie von sogenannten Curved Kites, deren Masse Fibonacci Zahlen entsprechen. Ein Curved Kite ist eine interessante geometrische Figur, die einem Stachelrochen, oder eben einem kurvenförmigen Drachen (engl. curved kite) gleicht.
Der Rand eines Curved Kites besteht aus drei Viertelkreisen. Die zwei gleichgrossen, kleinen Viertelkreise treffen sich im spitzigen Schwanz des Kites. Der grosse Viertelkreis verbindet die anderen Enden der kleinen Viertelkreise und trifft auf diese in einem 45° Winkel.
Wenn die kleinen Viertelkreise einen Radius r haben, dann hat der grosse Viertelkreis den Radius R = √2·r.
Ein Curved Kite hat die erstaunliche Eigenschaft, dass seine Fläche genau r² beträgt, wobei r eben der Radius der kleinen Viertelkreise ist. Folglich hat dieser kurvige Curved Kite die Fläche des Quadrats, in dem einer seiner Viertelkreise eingebettet ist. Damit zeigt der Curved Kite eine Art „Quadratur der Kreise“.
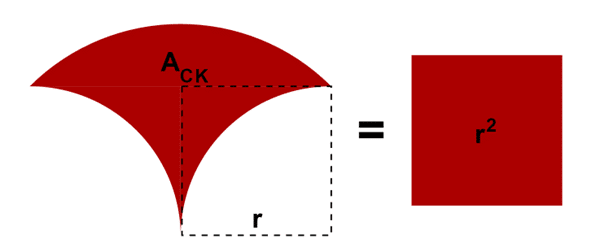
Foto: © 2024 Gauthier Cerf. All rights reserved.
Curved Kite Fibonacci Flower
Das Bild Curved Kite Fibonacci Flower entsteht aus einer Serie von je zwei gleich grossen, einander gegenübergestellten Curved Kites, deren Spitzen sich treffen. Alle Curved Kite Paare der Serie treffen sich im gleichen Punkt, sind aber jeweils um den goldenen Winkel 137.508º im Uhrzeigersinn gedreht. Kleinere Paare sind in hellerem Grün gehalten und erscheinen über den jeweils grösseren Paaren.
Ganz ähnlich machen das viele Pflanzen in der Natur, um die Beschattung ihrer Blätter minimal und das Sonnenlicht maximal zu halten.
Im Innern des so aus den Curved Kites geformten Blätterwaldes entsteht aus dem Hintergrund in eigener Gegenständlichkeit eine neue Blattpflanze, die entfernt einem Cannabis Blatt gleicht.
Weitere Bilder aus der Curved Kite Serie:
Weitere Fibonacci Flower Bilder:

